Tag: visualisation

Posted on

Correlation in Python

How to create a correlation heatmap in python
and some specialities for mutual funds data

After introducing the correlation matrix and heatmap in R I’ll show you here how to perform this task in python. See for yourself which code suits you better.

For the correlation in python I programmed the following three notebooks. The differences lie mainly in the data supply.

  1. correlation-in-python.ipynb: The basic python notebook that uses the same input data as the corresponding R example.
  2. correlation-ip-yfin.ipynb: The correlation in python that uses the yfinance API as data source.
  3. correlation-ip-fonds.ipynb The correlation in python example that uses data from ARIVA and adds some mutual funds.

Let’s start with the first notebook for the direct comparison to the correlation-in-R: The data is read from CSV files containing the columns ‘Date’ and ‘Close’. To have comparable data (i.e. every data set contains the same date-values) I merged the input files into the merged_quotes pandas dataframe. To keep the R code clean I manually merged the files there. But with pandas this can be done on the fly: 

merged_quotes = pd.merge(merged_quotes, quotes, on='Date')

If you want to check your merged data afterwards you should use the parameter ‘suffixes’ on the merge. Otherwise the columns will be named ‘Close_x, Close_y, Close_x, Close_y, …’. For the same reason I renamed the columns afterwards.

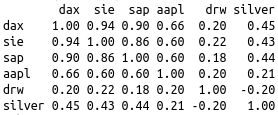
For the correlation matrix we need the percent changes from one day to the next. In the R-code this was “manually” done by the function getPVector (get performance vector). My Python code does this by applying pct_changes() to the complete dataframe (except for the column ‘date’, which was formerly dropped of course).

corr() calculates the correlation matrix on the percent changes. 

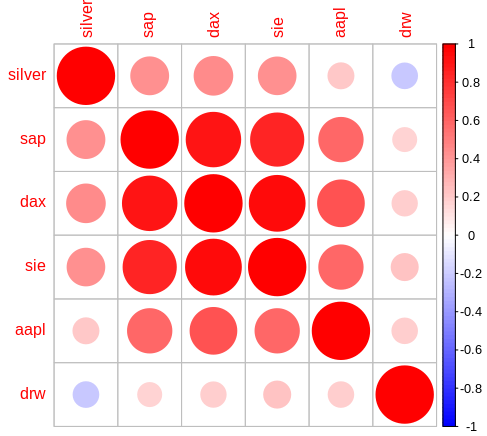
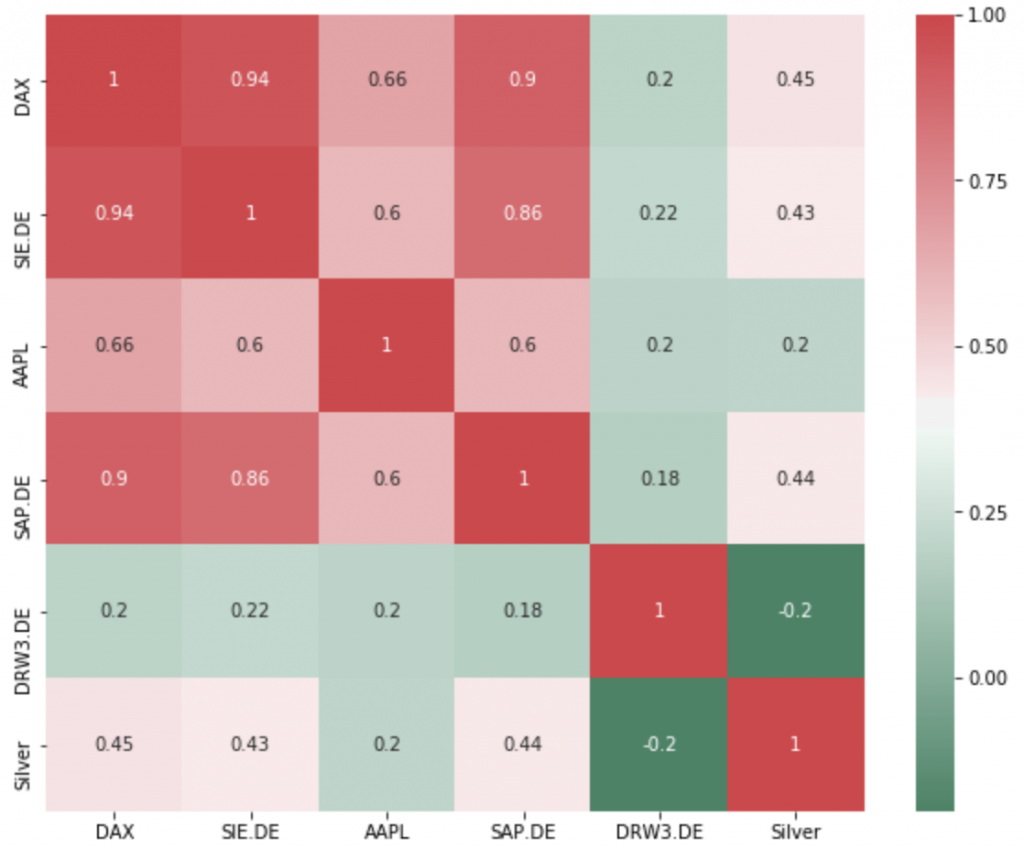
For the visualisation I used the easy to handle seaborn heatmap with a colour palette range from green to red. The parameter annot=True prints the correlation values in each square. If you prefer colours from blue to red you can simply replace the cmap by the value ‘coolwarm’.

Seaborn Correlation Heatmap
Seaborn correlation heatmap

The second code ‘correlation-ip-yfin’ loads the data from yahoo finance with the help of the yfinance api as described in my first post. Because it was so easy loading some more sets I made the entries list rather long. The fact that you only find a few really low correlations when using a 3-months-history is very interesting. And if you’re only looking at the correlation, the only suitable addition for any stock portfolio seems to be Drägerwerk, not only since the beginning of the corona crisis. But don’t forget to consider the performance.

The third notebook ‘correlation-ip-fonds.ipynb’ loads mutual funds and ETF data from previously downloaded files from ARIVA.DE. To retrieve the data remove the *.csv-files from the data-funds directory and execute the scripts there:

  • getQuotes.sh to download the data as [wkn]_historic.csv. You can use min_date and max_date to retrieve a certain period of data (e.g. getQuotes.sh 19.09.2019 03.04.2020)
  • revertFiles.sh to convert the data in usable format (date and close, order: from old to new)

This code has one special feature: after the first runs I realised that the ÖKOWORLD funds had a surprisingly low correlation. A closer look revealed that they apparently report their values one day later. So the data from these funds must be shifted by one day.

The funds are surprisingly high correlated. Even the MSCI World, the Emerging Markets and the Scandinavian funds. If you happen to find high-performance funds with lower correlations or an API for easier funds-data-download, please let me know.

Source

https://github.com/ds4pi/correlation-in-python

Posted on

Correlation in R

Pick your stocks by Correlation –
Develop and visualise your portfolios’ correlation matrix in R

Modern portfolio theory has proven the fact that adding stocks with different price movements reduces your portfolios’ overall risk when other factors stay constant (i.e. performance). Stocks that react differently to external influences (e.g. oil price shocks or FED interest rate decisions) are less correlated with each other.

This correlation can be measured with statistical methods. The basic measurement for the joint variability of two variables is the covariance. The standardized measurement is the Pearson correlation coefficient that ranges from -1 to +1. A coefficient of +1 means perfect synchronical movement of both variables in the same direction, while -1 indicates perfect sync in different directions. A coefficient value of 0 states no relationship at all between the movements of both variables.

When looking for uncorrelated stocks as an addition to our existing portfolio we are therefore looking for stocks with small absolute values of their correlation coefficient with any other position in our portfolio. The instrument of choice is the correlation matrix and the visualisation is the correlation matrix’ heatmap.

Both are not hard to implement with some lines of R code.

First we download the historical data for the different stocks as described in the yfinance article and save it in the data directory. The historical data need some steps of preparation:

  • align the entries so that we have the same days for all stocks
  • remove everything but the close values from the files

Additionally the quotes must be sorted from old to new values (what is given if you download them by yfinance).

For this example I added historical data from silver (ticker symbol SI=F) to show an example of commodity correlation to stocks. Other values you’ll find in the data subdirectory are from common stocks like SAP, Apple and Drägerwerk. (If you find an API to reliably download mutual funds data please let me know).

The code starts by loading the corrplot package for plotting the correlation heatmap. Next is the function getPVector that returns a vector of performance values.

To have comparable values for the stocks we can’t take the raw quotes. But with the daily returns (daily performances) we have comparable movement variables regardless if we consider stocks, indices, funds or commodities. The daily performance is calculated by

\[p_{t}=\left(\frac{quote_{t}}{quote_{t-1}}-1\right)\times100\textrm{  [Performance in %]}\]

which equals

\[p_{t}=\frac{quote_{t}-quote_{t-1}}{quote_{t-1}}\times100\]

That’s what is implemented in getPVector.

Next there is the function to read the stock quotes (importPVector) and return the performance vectors which is then done by the lines starting with

dax <- importPVector("DAX.csv")

After importing we combine the vectors to the matrix ‘mat’ and as result retrieve the correlation matrix by using cor(). For better readability this matrix is rounded to two digits. And looks like this:

correlation matrix
Correlation matrix

The last two code lines build the correlation matrix’ heatmap.

correlation heatmap from corrplot
Correlation heatmap from corrplot in R

What do we do with these results?

  • The large red circles next to the diagonal identify our portfolios’ cluster risks. We can then think about repositioning in favour for less red circles (i.e. sell combined risks and rebuy positions with less correlations).
  • Next we see the fantastic low correlation with the small cap DRW (Drägerwerk) and DAX. The overall correlation with this stock and the other values is even better than the correlation with silver and the other values.
  • Check for suitable additions: you can now add and check buying candidates (and if you own large DAX-Index positions it will be clear not to add other large DAX stock positions like Siemens).
  • Try to download your ETF or mutual funds’ close values and check single stocks as candidates for correlation. Also check other funds as possible additions for correlation with your existing portfolio.
  • Check commodities (gold, silver, oil, …) as add-ons for your portfolio.
  • Find a way to reflect the combined position sizes in den heatmap fields (i.e. large circles for large positions, small circles for small positions). Then think about your large red circles in order to reposition your assets.
  • But if you find additions with minimum correlation to your existing portfolio positions don’t forget to think about the performance chances of that candidates!

Source

https://github.com/ds4pi/correlation-in-r

Links

Modern Portfolio Theory – systematic and specific risk
Pearson correlation coefficient
https://github.com/taiyun/corrplot
https://cran.r-project.org/web/packages/corrplot/